The goal of causal inference is to understand the effect of an intervention. We want to estimate the difference between what happens if people receive a treatment compared to what would have happened if they hadn’t been treated.
Some examples of this include:
- We could be interested in the causal effect of an advertising campaign on some kind of conversion event, like purchases.
- One example of a causal question we could ask is: how much extra money does seeing an ad cause someone to spend, compared to what they would have spent if they hadn’t seen the ad?
- In Section 8 of my difference-in-differences paper, I analyze the data from a 2006 paper that estimates the causal effect of no-fault divorce laws on violent outcomes.
- In this case, the causal question is how do violent outcomes compare if a state passed no-fault divorce laws to the outcome if a state hadn’t passed that law (but everything else, like cultural and economic factors and so on, was the same)?
- We might want to know if multivitamins improve health outcomes.
- For example, we could ask if taking multivitamins causes people to live longer, compared to how long they would have lived if they had done everything else the same but not taken multivitamins.
Why Is Estimating Causal Effects Tricky?
Let’s focus on the multivitamin example. Some examples of ways that we can’t answer this question include:
- Comparing the mortality rates of people who choose to take multivitamins to people who don’t. This doesn’t work because people who choose to take multivitamins might have healthier habits overall, or may simply have more resources to commit to their health.
- Maybe the vitamin-takers are on average also get better sleep, exercise more, eat healthier, etc. So some of the difference in outcomes between those two groups will be due to the vitamins, and some will be due to the difference in overall healthy behaviors. In economics this is called selection bias (and it can be characterized mathematically).
- Selection bias is a problem for us because we’re interested in isolating the effect of the multivitamin itself.
- When we simply compare outcomes between the two groups, we’re not isolating the effect of multivitamins, we’re seeing the total effect of all the differences between these two groups—both the differences we’re aware of and the ones we’re not.
- (More sophisticated studies can attempt to control for variables like reported alcohol consumption, blood pressure, etc. But this kind of thing is not always reliable–often we can’t control for every last thing that could influence health outcomes.)
- Comparing outcomes before and after beginning to take multivitamins. People use this kind of “before-and-after” reasoning all the time in everyday life—they try implementing a change and they see if they notice a difference. But it’s not always reliable, and it’s definitely not scientifically valid for a formal study, for two reasons.
- First of all, there might be a selection bias issue.
- If you choose to start taking a multivitamin in April, it may be because you had a sudden increase in your motivation or ability to take care of your health. Maybe around the same time you start taking a multivitamin, you also implement other changes to improve your health.
- So again, we can’t disentangle how much of the difference in your health outcomes is due to the vitamins and which are due to other changes in your behavior.
- Relatedly, we don’t know what your outcome would have been had you done everything else the same but not taken multivitamins.
- Let’s say we want to examine the slightly different research question of whether multivitamins protect people from catching a cold. We could randomly select people to take multivitamins in April. Assuming everyone in our study cooperates with their assignment to take multivitamins, there wouldn’t be a selection bias issue when we compare their April and March health outcomes.
- However, what we want to know is the difference between their April health outcome had they taken vitamins versus had they not taken vitamins. We might see that everyone who took vitamins got fewer colds in April than in March. But maybe that had nothing to do with the vitamins—it was just because cold and flu season was ending.
- (By the way, we can also handle situations where not everyone cooperates with their assigned treatment, but that opens up a whole other can of worms that I intend to discuss another time.)
- First of all, there might be a selection bias issue.
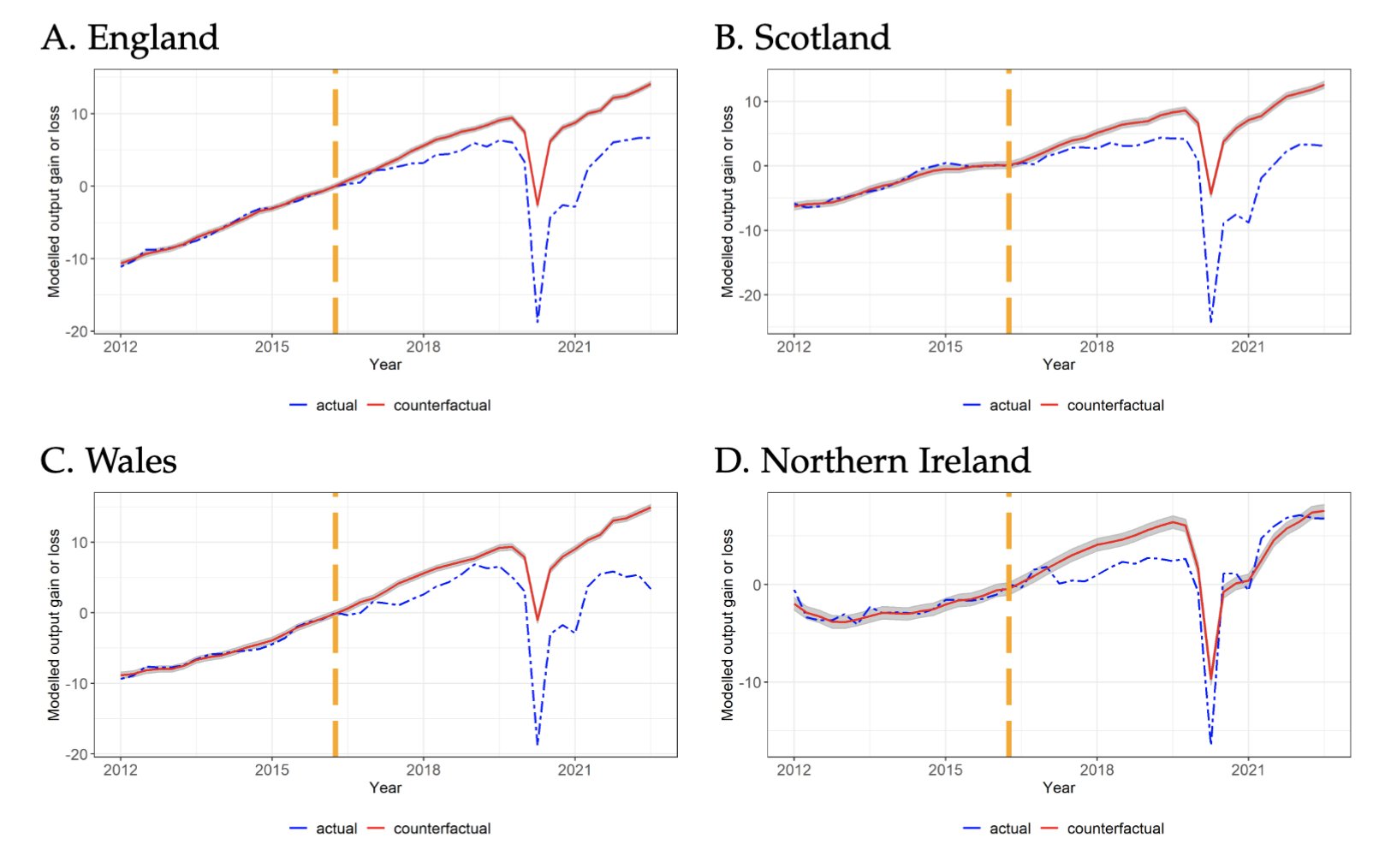
I’ll give one more example to drill down into the issue of what counterfactual outcomes we are interested in. Recent research has investigated the causal effect of the United Kingdom’s 2016 vote to depart from the European Union (“Brexit”), which was implemented in 2020. Using the synthetic controls method, the researchers compared the economic production of countries that didn’t leave the European Union in order to estimate what would have happened had the U.K. stayed in the E.U. You can see some of the resulting charts below. The gap between the actual (blue dashed) and estimated counterfactual (red solid) lines is the estimated causal effect of Brexit on economic production.

So what is a valid way to estimate the effect of an intervention?
A really important part of causal inference is thinking very carefully about exactly what it is that you’re trying to estimate (the estimand), then defining it precisely. All of the issues above can be traced to imprecise thinking about what it is that we actually want to learn. Of course, what you might want to learn in a given situation depends a lot on the particular circumstances you’re in and personal preferences, so there’s really no substitute for understanding causal inference concepts and careful consideration of your situation. Applying off-the-shelf methods thoughtlessly can lead to very misleading results.
That said, there’s been a lot of work in causal inference over the years and a relatively small number of estimands have been found to be useful in a wide variety of situations. So usually you don’t have to re-invent the wheel to get an estimator that is appropriate for your situation.
Randomized controlled trials (RCTs), sometimes called randomized experiments or A/B tests in the tech industry, are often called the “gold standard” methodology in causal inference. In this case, we randomly assign units to either be treated or not.
- The randomization ensures that we don’t have selection bias.
- Comparing treated units to control units (as opposed to the treated units’ own pre-treatment outcomes) ensures that we avoid the time-based issues I mentioned above.
By the way, to get to the punchline on the multivitamin question (and please keep in mind that I am not an expert on nutrition, and I’m sure someone who is would tell you that the complete truth is more nuanced than this):
- There are plenty of observational studies indicating that people who take multivitamins tend to be healthier than those who don’t.
- That is, if we ask the question “are people who choose to take multivitamins generally healthier than people who don’t?” the answer seems to be “yes.”
- However, RCTs generally show that taking multivitamins doesn’t seem to have a measurable effect on health outcomes for people who don’t have other health issues that specifically make taking a multivitamin advisable.
- So if we ask the question “if we somehow could get people who don’t have clear signs of malnutrition and don’t currently take a multivitamin to start taking one (maybe by giving away vitamins for free, or getting press coverage about the importance of taking multivitamins, or getting supplement companies to advertise them aggressively), would taking those vitamins improve health outcomes in the people who started taking them?” broadly speaking the answer seems to be “no.”
- Same story if we ask the question “if people who currently take multivitamins but don’t have a clear medical need for them stopped taking them suddenly but did everything else the same, would we expect to see a measurable change in their health outcomes?”
So, it seems like the association between taking multivitamins and good health outcomes might be mostly due to selection bias.
Observational Causal Inference
Causal inference on non-experimental (observational) data is much trickier. But it’s often necessary because an RCT is not practical or even possible, whether due to ethics, cost, or the nature of a particular intervention.
- Clearly an experiment where we randomly force some people to start smoking would be unethical, for example. In fact, some of the earliest modern work in observational causal inference came from trying to prove a causal link between smoking and lung cancer without a randomized experiment.
- One domain where experiments often aren’t possible is public policy–no experiment would allow us to measure the effect of Brexit, for example.
- Another example from the tech industry: maybe you want to know the effect a new version of your software has on some outcome, like engagement or conversions. Generally you can’t force your customers to update their software, so it would probably be most practical to rely on observational causal inference techniques.
- Lastly, in advertising you could do various kinds of A/B tests to test the effect of an ad, but you can’t really make people actually see the ad. (Maybe they won’t visit the website where the ad is displayed during the experimental period, for example.) This touches on the “non-cooperation” problem I mentioned earlier. For now, the important thing to keep in mind is that this is a situation where people have some say in whether they receive the treatment or not, so we need to use some kind of observational causal inference techniques if we want to know the effect of the treatment.
Observational causal inference techniques include controlling for confounding variables, using event study techniques like difference-in-differences or synthetic controls, or taking advantage of other kinds of natural experiments using techniques like instrumental variables or regression discontinuity designs. I’ll talk more about some of these other techniques in future posts.