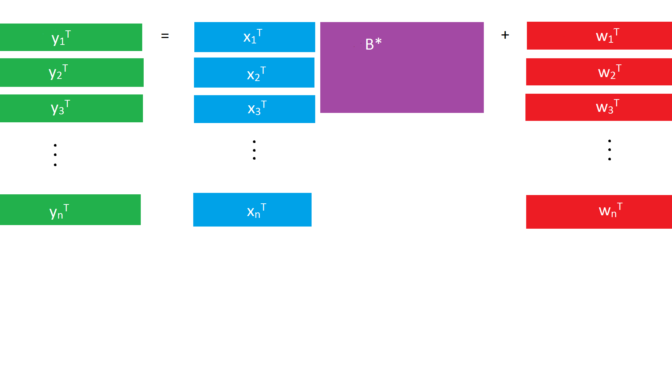
Today I gave an in-class presentation at USC on two papers in multi-task learning (or multivariate regression–linear regression when the response is a vector rather than one number). You could simply train a separate model for each response, but when the responses are related, there are advantages to considering them all at the same time and building one big model.
Each paper covered a different approach to feature selection for linear regression with multivariate responses under the assumption of sparsity. Obozinski et al (2011) imposes sparsity in the union of the supports by imposing a group lasso penalty on each feature across every response (corresponding to rows of the coefficient matrix). Chen et al (2012) instead examine the singular value decomposition (SVD) of the coefficient matrix and impose sparsity in the left and right singular vectors in each SVD layer (relaxing orthogonality to achieve sparsity).
My slides along with the notes I used for the presentation are available to read here on my Github. Feel free to reach out with any questions!
These are the papers I presented:
Obozinski, Guillaume; Wainwright, Martin J.; Jordan, Michael I. Support union recovery in high-dimensional multivariate regression. Ann. Statist. 39 (2011), no. 1, 1–47. doi:10.1214/09-AOS776. https://projecteuclid.org/euclid.aos/1291388368
Chen, K. , Chan, K. and Stenseth, N. C. (2012), Reduced rank stochastic regression with a sparse singular value decomposition. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 74: 203-221. doi:10.1111/j.1467-9868.2011.01002.x